| Fractal Art |
| News |
| Eigene Fotos drucken |
| Foto Editor |
| Fraktal Galerie |
| Kalender |
| DVDs |
| Grusskarten |
| Bilderbände |
| |
| |
Warenkorb  |
| Fractal Sience |
Interaktive Tools |
| Theorie |
| Links |
| |

|
|
Unbenanntes Dokument
Unbenanntes Dokument
| |
Inhalt
1. Chaos
Eine wachsende Anzahl von Wissenschaftlern entwerfen heute
neue, gewagte Perspektiven: «Der Aufbau und das Verhalten lebender Systeme
sind in ihrer Variabilität und Kompliziertheit gleichermassen dem Chaos
wie einem regelmässigen Muster nahe.» Mit Hilfe des Computers zeigen
sie uns, was man erst zu lernen beginnt die Gesetze des Chaos,
der Unregelmässigkeit, des Unvorhersagbaren, welche hinter den meisten
Dingen unserer Welt stehen (der menschliche Herzschlag und menschliches
Denken, Wolken und Gewitter, die Strukturen der Galaxien, das Entstehen
eines Gedichtes, die Ausbreitung eines Waldbrandes, eine gewundene Küstenlinie,
Ursprung und Evolution des Lebens). Auf welche Weise Ordnung zerfällt
und ins Chaos übergeht und wie Chaos Ordnung schafft, hier überschneiden
sich die wissenschaftlichen Disziplinen. Das gemeinsame Werkzeug aller
Chaosforscher ist aber der Computer.

In der Alltagssprache gilt Chaos als das Gegenteil von Ordnung.
Griech. = gestaltlose Urmasse. Nach Hesiod (700 v.Chr.) war im Anfang
das Chaos (die grenzenlose, gähnende Leere) aus der Gaia (die Erde)
entstand. In der Bibel: « ...und die Erde war wüst und leer». Alte Völker
glaubten, die Kräfte des Chaos und der Ordnung seien Teil einer unbehaglichen
Spannung. Dabei dachten sie an etwas Unermessliches und Kreatives. Die
ägypter stellten sich das frühe Universum als einen gestaltlosen Abgrund
namens Nut vor. Nut gebar Ra, die Sonne. In einer chinesischen Schöpfungsgeschichte
entspringt ein Strahl reinen Lichts, Yang (männliches Prinzip), dem
Chaos und errichtet den Himmel, während das zurückbleibende schwere
Trübe, Yin (weibliches Prinzip), die Erde bildet. Zuviel Yin oder Yang
wird das Chaos zurückbringen. Die mythische Vorstellung beruht also
auf der Vorstellung, dass die kosmische Schöpfungskraft auf einer wechselseitigen
Beziehung zwischen Ordnung und Unordnung beruht. Im Modell erscheint
die Ordnung als kleiner Bereich innerhalb eines weiten Feldes des Chaos.
Im Chaos gibt es Inseln der Stabilität. Mathematiker, Naturwissenschaftler
reden von «chaotischen» Systemen, wenn deren Entwicklung nicht determiniert,
nicht vorhersagbar ist. Paradox erscheint der Begriff «deterministisches
Chaos», welches auf den ersten Blick als blosser Zufall erscheint, aber
streng gesetzmässig entsteht (z.B. in Turbulenzen). Trotzdem ist das
Verhalten deterministisch chaotischen Systeme nicht berechenbar, da
sie auf kleinste Veränderung der Anfangsbedingungen reagieren. (Geo
Wissen 93)
Im rationalistischen-mechanistischen Weltbild hatte das
Chaos in der Wissenschaft keinen Platz. Erst die «unlösbaren» Aufgaben
in der Mathematik öffneten die Türen und machten chaotische Vorgänge
Paradoxa, Turbulenzen in Mengen verständlich und sichtbar. Chaotische
Prozesse können durch geringste Veränderungen ausgelöst werden. Ein
labiles Gleichgewicht verwandelt sich plötzlich in ein grosses Ungleichgewicht.
Die bestehende Ordnung beginnt plötzlich «ver - rückt» zu spielen. Das
Chaos kann in allen Lebensbereichen auftreten und ist aber nicht programmierbar.
Die Angst vor dem Chaos können wir nur bewältigen, indem wir seine Unvorhersehbarkeit
akzeptieren.

1.1 Beispiele für chaotische Erscheinungen:
- Rauchfahnen: Zuerst steigt Rauch (Zigarette, Raucherstäbchen)
linear auf. Bald erreicht er aber eine Stelle, wo er sich wirbelnd
auszubreiten beginnt.
- Wetter: Lange meinte man, es wäre mit genügend Daten von
vielen Messstationen möglich, den Austausch von Hoch- zu Tiefdruckgebieten
zu berechnen und somit das Wetter längerfristig vorherzusagen. Die
kleinste änderung eines Faktors, der das Wetter beeinflusst, kann
aber unerwartete und chaotische Auswirkungen haben.
- 3. Weltall: Einst glaubte man noch an die Sphärenharmonie
und an die Idee, dass im All alles schön rational geordnet seine
Bahnen zieht. Heut kennt man aber Hyperion (einen Saturnmond), der
«chaotisch» herumtorkelt.
- Tropfenbildung am Wasserhahn: Nach logischer überlegung
müsste der Wasserstrahl nach unten immer dünner werden, - er bildet
aber Tropfen.
- Verkehrschaos: Beim wachsenden Verkehr wird alles nicht
einfach etwas langsamer, sondern irgendwann nach chaotischen Schnell-
und Schleichphasen kommt plötzlich der Zusammenbruch.
- Klimaumschlag in Südamerika «El Niño: In Südamerika gibt
es ein Gebiet, in dem zeitweise das Klima durch das Ansteigen der
Temperatur um mehrere Grade umkippt, was zu Folgeschäden wie Tiersterben
führt.
- Pendel: Ein Pendel, das ich an einer zweiten Schur aufhänge,
entwickelt je nach Anfangsimpuls ganz andere chaotische Schwingungen.
Die Bahn eines chaotischen Pendels ist nicht mehr im voraus berechenbar.
Wenn wir es loslassen, folgt es zuerst den mechanische Gesetzen.
Kleinste änderungen bewirken etwas Unvorhersagbares (Schmetterlingseffekt),
und die Kausualität stimmt nicht mehr.
- Wirbelbbildung im Fluss, Bergbach, Kanal: Im Kanal fliessen
zwei gleiche Bretter mit einer starken Kausualität (vorhersagbar).
Im Bach mit Steinen aber ist keine Aussage möglich.
- Modell Fuchs/Maus: x1 = ax (1 - x) > Formel mit
Ausgangspunkt Fuchspopulation (x1), Bremsterm (1-x) zur Rückkoppelung.
Wovon hängt die Entwicklung ab? Von der Anzahl der Anfangstiere?
Nein: Vermehrungsfaktor! Mehr Füchse > weniger Mäuse, keine
Mäuse > Aussterben der Jäger. Chaotische Entwicklungserscheinungen
mit scheinbar stabilen Zwischen-phasen, bis einmal plötzlich der
Systemzusammenbruch kommt. Was ist effektiv und wie beeinflussbar?
- Wellenbildung
- Plötzliche Naturgewalten
- Videorückkoppelung
- Börse
- Wirtschaft
- Leben, Krankheit, Herzstillstand, Tod
- Lehren und Lernen

1.2 Nichtlineare Gleichungen
In nichtlinearen Gleichungen kann die änderung einer variablen
eine völlig, ja katastrophale Auswirkung auf andere Variablen haben.
Zum Beispiel kann man damit beschreiben, wie dein Erdbeben losbricht,
wenn zwei Platten an der Oberfläche der Erdkruste gegeneinander drücken.
Die dabei entstehende Spannung kann jahrzehntelang allmählich ansteigen,
bis plötzlich ein «kritischer» Wert erreicht wird. In der nichtlinearen
Welt sind aber exakte Vorhersagen praktisch wie theoretisch unmöglich.
Mittels Modellen lassen sich aber in Systemen kritische Punkte aufspüren,
in denen eine kleine Veränderung grosse Wirkung hervorbringen kann.

1.3 Attraktor
In einfachen, regelmässigen Systemen tritt periodisches
Verhalten auf (periodische Schwingungen mit wiederkehrender Rückkehr
zu den Anfangsbedingungen (Violinsaite, Pendel, Tag und Nacht). Die
Schwingungen eines Pendel bewegen sich von vom grössten Ausschlag links
(Impuls Null) zum tiefsten Punkt (grösste Geschwindigkeit) zum grössten
Ausschlag rechts (Impuls Null). Im Phasenraum dargestellt, strebt das
Pendel durch den Luftwiderstand gebremst dem Ruhepunkt zu. Diesen Punkt
nennen die Mathematiker einen Anziehungspunkt oder «Attraktor». Der
Attraktor ist also ein Gebiet im Phasenraum, das eine Anziehungskraft
auf ein System ausübt. Ein chaotischer Attraktor besitzt eine selbstähnliche,
fraktale und nicht vorhersehbare Struktur und Lebensdauer. Der Ablauf
seiner Bahn ist empfindlich von Anfangsbedingungen abhängig. Es können
mehrere Attraktoren gleichzeitig existieren. Unwesentlich erscheinende
Attraktoren können blitzschnell ungeahnte Effekte herbeiführen. Attraktoren
im Chaos sind zeitlich begrenzt, da sich während einer Stabilitätsphase
alle nicht am Attraktor beteiligten Faktoren weiterentwikkeln und den
Attraktor irgendwann zu Ende führen. Zusammenbruch >Verunsicherung,
Neuorientierung, Angst vor Chaos, ...
Beispiele für Attraktoren:
- Wurzelziehen: Irgendeine Zahl wählen und mehrmals die Wurzel ziehen:
> immer 1. Nach vielen Iterationen (Rückkoppelung) zielt
die Zahl immer gegen den Attraktor 1.
- Chaotische Pendel: Ein Pendel schwingt immer auf die grösste Höhe
links und rechts aus (dort Geschwindigkeit 0). Aber schlussendlich
pendelt es unten aus (Attraktor).
| |
Lorenz-Attraktor:
Lorenz entdeckte 1960 das nichtlineare dynamische System
des Wetters. Ein mit Messungen bestimmter Anfangspunkt (Zustand)
erhält durch die Verknüpfung mit dem Gesamtsystem eine unermessliche
Unbestimmtheit. Der wahre Zustand kann in jedem Punkt des
Attraktors liegen. Bsp. Wetter - lokal unvorhersagbar, aber
global stabil.
|

1.4 Turbulenz
Turbulenzen treten überall in der Natur auf (Luftströmungen, Lava,
Umspülung von Steinen, Wetterkatastrophen) und stellen die Menschen
oft vor grosse Probleme. Bei gleichmässig fliessendem Wasser entstehen
stabile Wirbel, die einen punktförmigen Attraktor haben und nach Störungen
zum gleichen Grundmuster zurückkehren. Bei zunehmender Strömungsgeschwindigkeit
werden die Wirbel instabil, fransen aus (Grenzzyklus), und zuletzt
scheint jedes Wasserteilchen (Wirbel im Wirbel im Wirbel) sich zufällig
und chaotisch zu bewegen (seltsamer Attraktor).

1.5 Iteration, Rückkoppelung
Von at. «iterare» = gebrochen. Rückkoppelung durch Wiederaufnahme
und Wiedereinbeziehung von allem, was vorher war (Bsp.: Erneuerung
aller Körperzellen in etwa 7 Jahren, künstliche Intelligenz, Wettersysteme).
Wiederholte Anwendung einer Rechenvorschrift, wobei jedes Ergebnis
als Ausgangspunkt für den nächsten Schritt dient. Negative (hemmende)
und positive (verstärkende) Rückkoppelungen entdeckte man bei Mikrophonen,
die zu nahe am Lautsprecher sind und durch das Rückschicken des aufgefangenen
Tones auf den Verstärker ein chaotische Geräusch produziert. Rückkoppelung
ist Spannung zwischen Ordnung und Chaos. Rückkoppelungen kommen überall
auf vor: Auf allen Ebenen des Lebendigen, in psychologischen Abläufen,
in der Evolution des ökologische Gesamtsystemes und in mathematischen,
nichtlinearen Gleichungen.

1.6 Beispiele Iterationen
- Zahlenverdoppelung (exponentielles Wachstum). x1 = 1, x2 = 2, x3
= 4; 8, 16, 32, x1 = 1.5, x2 = 3, x3 = 6; 12, 24, 48,
- Verdoppelung der Zahlen mit Weglassen des ganzzahligen Anteils
x1 = 0.9134, 2xn = 1.9134 > 0.9134; x1 = 0.707070; 0.414141;
0.828282; 0.656565; 0.313131; 0.626262; 0.252525; 0.505050; 0.010101;
0.020202; 0.040404; 0.080808; 0.161616; 0.323232; 0.646464; 0.292929;
0.585858; 0.707070. Nach 17 Iterationen landen wir bei der Ausgangszahl.
- x1 = 0.707070; Wenn wir in der 4. Dezimalstelle einen kleinen Fehler
machen > 0.707170 bläht sich der Fehler bis zur 11. Iteration
so auf, dass sich die Zahlenfolge vollständig von der ursprünglichen
entfernt. 0.707170; 0.414341; 0.828682; 0.657365; 0. 314731; 0.629462;
0.258924; 0.517849; 0.035698; 0.071396; 0.142792; 0.285584
- Nicht nur Gleichungen haben eine extreme Empfindlichkeit gegenüber
ihren Anfangsbedingungen. Forscher beobachten dieselbe Dynamik in
Flüssigkeiten. Bsp. Kleine Wirbel im Blutstrom, in dem bebachbarte
Punkte nebeneinander herfliessen oder in völlig anderen Bereichen
der Flüssigkeit landen können (Schmetterlingseffekt).
- Das Dehnen und Falten im Teig eines Bäckers zeigt bildhaft die
Bewegungen, wie sie in nichtlinearen Iterationen vorkommen. Benachbarte
Punkte des Teigs geraten auseinander, und es entsteht ein komlipziertes
, unvorhersagbares Muster.
- Seltsame Attraktoren und Iterationen sind mitten in Ordnungen anzutreffen
und können Phänomene wie einen Herzanfall bewirken.

1.7 Beispiel algebraische Iteration
Eine Iteration liegt vor, wenn mit einer Zahl eine Rechnung ausgeführt
wird, dann mit dem Resultat als Ausgangspunkt dieselbe Rechnung, mit
dem neuen Resultat wiederum dieselbe, usw. Die Iteration und die damit
verbundene Rückkopplung stellt eines der wichtigsten «Werkzeuge» bei
der Entwicklung mathematischer Fraktale dar. Das Prinzip der Rückkopplung
und der Iteration ist sehr alt. Es war bereits den sumerischen Mathematikern
vor rund 4000 Jahren bekannt (beispielsweise benutzten diese iterative
Schritte zur Berechnung der Quadratwurzel einer Zahl).
Mit dem Taschenrechner und dem Begriff Quadratzahl können wir einen
ersten Einblick gewinnen. Es wird eine reelle Zahl c als Konstante
gewählt und nun eine Zahlenfolge hergestellt.
a0 = 0 Mit der Ausganszahl a0, hier der 0, beginnend, wird eine Rechenoperation
a1 = a02 + c ausgeführt, mit dem Resultat dieselbe, usw. Kurz: Es
wird eine Folge von
a2 = a12 + c Iterationen berechnet.
Im allgemeinen strebt die Folge gegen ƒ oder einen durch c bestimmten
Grenzwert, den wir g(c) nennen. So erhalten wir z.B. g (0,2) ª 0,28
und g (-0,5) ª-0,37. Trägt man g(c) über c in ein Koordinatensystem
ein, ergibt sich so zunächst eine Kurve. Geht man aber zu kleineren
(c) über, dann tritt etwas überraschendes ein. Bei (c) -1,1 etwa pendeln
sie Folgenglieder, die mit geradem Index streben gegen eine andere
Zahl, als die mit ungeradem Index. Man nennt diese Zahlen Attraktoren,
weil sie die Zahlen der Folge gleichsam anziehen. Im Achsenkreuz verzweigt
sich die Kurve nach links. Zu einem c gehören nun zwei Zahlen g(c).
Bei übergängen zu noch kleineren c-Werten zeigt sich, dass sich auch
diese Zwei wieder verzweigen. Wir erhalten dann 4 Attraktoren, danach
8, Š . Bei etwa c ‚ -1,5 ergibt sich eine völlig neue Situation. Nun
ist überhaupt keine Struktur zu erkennen. Man spricht von der Strukturlosigkeit
des Chaos. Der Mathematiker Feigenbaum stellte dies in seinem «Feigenbaumdiagramm»
dar (siehe Werkstattposten Chaos, Bifurkation). Wir untersuchen nun,
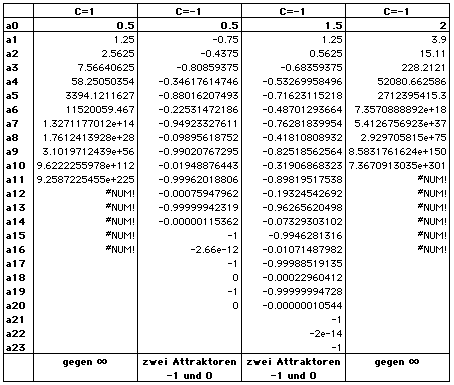
was kleine änderungen im Rechenprozess (an+1=an2+c) bewirken, wenn
wir für a = (0.5/1.5/ und C= (1/-1/) einsetzen. Das Ergebnis der zweiten
Iteration (a = 0,5; C = -1) ist überraschend. Es entstehen zwei Folgen
mit verschiedenen Grenzwerten, nämlich -1 und 0. Man nennt diese beiden
Zahlen Attraktoren (attrahere = heranziehen). Bei der Ausgangszahl
a = 1,5 führt zu den gleichen Attraktoren, aber die Ausgangszahl 2
strebt gegen ƒ.
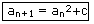

Die Entdeckung, dass zwei sich beliebig wenig voneinander unterscheidende
Zahlen sich bei der Iteration völlig verschieden verhalten, also zu
gänzlich anderen Ergebnissen führen, kann mit bestimmten Situationen
in der Natur verglichen werden. So können zwei eng benachbarte Regentropfen
über einer Wasserscheide in die Nordsee oder in das Mittelmeer gelangen
(Schmetterlingseffekt).

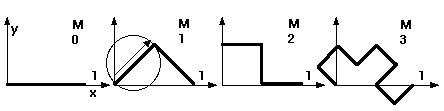
1.8 Die geometrische Iteration
Fraktale kann man auch rein geometrisch gewinnen, indem man von einer
einfachen Punktmenge M0 ausgeht. An ihr werden nun gleichzeitig mehrere
Abbildungen vorgenommen und die Bilder zu einer neuen Punktmenge M1
vereinigt. Im nächsten Schritt wird mit M1 ebenso verfahren.
1. M0 wird um 0 im Verhältnis 1:÷2 zentrisch gestreckt und um 0 um
45° gedreht.
2. M0 wird in derselben Weise gestreckt, aber nun um 0 um 135° gedreht
und um 1 nach rechts verschoben.

1.9 Bifurkation
Wenn die Geburtenrate einer Tierpopulation unter 1 ist, wird die
ganze Population auf 0 abfallen und erlöschen. Ist sie aber grösser,
wir sie zunächst abfallen, um sich dann auf einem konstanten Wert
(ca. 2/3 der ursprünglichen Grösse) einpendeln. Es scheint, dass 66%
ein Attraktor geworden ist. Bei einer Erhöhung der Geburtsrate auf
den kritischen Wert 3,0 passiert etwas Neues. Der Attraktor 0,66 wird
instabil und spaltet sich in zwei, d.h. die Population nähert sich
nun nicht mehr einem Wert, sondern schwankt zwischen zwei stabilen
Werten hin und her. Bei einer weiteren Erhöhung über 3,4495 ergibt
sich eine neue Spaltung (4 Werte) und ab 3.56 haben wir Bifurkation
in acht Fixpunkten (Periodenverdoppelung). Ab 3,56999 wird die Anzahl
der Attraktoren unendlich gross und endet im Chaos.

2. Fraktale
Von lateinischen « frangere, fractum» = brechen, gebrochen.
Mit Hilfe der fraktalen Geometrie lassen sich Ordnungsprinzipien im
Chaos zeigen. Der Begriff wurde 1975 vom Mathematiker Benoit Mandelbrot
geprägt. Fraktale sind oft selbstähnliche Gebilde, deren Ränder nicht
glatt, sondern unendlich rauh sind. Jede Vergrösserung zeigt wiederum
neue, ähnliche Strukturen (Apfelmännchen). Das Aussehen im Detail
wird in immer kleineren Skalen beibehalten. Fraktale Gebilde haben
eine gebrochene Dimension (Würfel = 3 Dimensionen). Viele natürlichen
Formen und nichtlineare Systeme haben fraktale Eigenschaften oder
verhalten sich fraktal (Wolken, Gebirge, Bronchien, Pflanzen, Galaxien,
Küstenlinien, Lunge, Wetter, Blutkreislauf, Gehirne). Die Anziehungskraft
der Fractale liegt vermutlich darin, dass in jedem seiner «Teile»
ein Bild des Ganzen enthalten ist.

2.1 Beispiele von Fraktalen
-
Z2+C = irgend eine beliebige Zahl. Diese Formel
schickt der Computer auf eine Reise in die Mandelbrot-Menge. Z
ist eine komplexe Zahl, die sich ändern kann, und C ist eine feste
komplexe Zahl. Der Computer muss das Ergebnis der Addition in
der nächsten Runde für Z einsetzen.
-
Nach Mandelbrot zeigt sich die fraktale Struktur
von Turbulenzen, dass sie in Böen auftritt. In einer stürmischen
Nacht wird der Wind plötzlich nachlassen, dann wieder aufleben,
Blätter kreisen lassen, bis sie wieder niedersinken.. Diese Turbulenzen
wiederholen sich in immer kleinerem Massstab.
-
Auch die von Lorenz als chaotisch erkannten Verhaltensmuster
des Wetters hält man heute für fraktal.
-
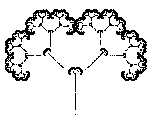
Die Verzweigungen eines lebenden Baumes sind offensichtlich
fraktal. äste haben Zweige, diese haben wieder kleinere Zweige,
und die Details wiederholen sich bis zum kleinsten Zweiglein.
Leonardo da Vinci stellte dazu schon fest, dass die äste bei fortschreitender
Verzweigung gerade so dünner werden, dass die Gesamtdicke (alle
äste zusammengepackt) insgesamt gleich bleibt.
-
Fraktale acht- bis 30fache Verzweigungsstruktur
der Venen und Arterien zur Blutversorgung. Fraktale Selbstähnlichkeit
durchzieht die Körper der Organismen. Der Körper ist eine Vernetzung
von lauter selbstähnlichen Systemen.
-
Kunst: Labyrinthe, iterative Sprachspiele, Gesangsmuster,
raffiniert verflochtene keltische Zeichnungen, archetypische Muster
auf rituellen, alten Gefässen rufen in uns oft das Gefühl des
Wiedererkennens (des schon Gesehenen) hervor und hängt mit Fraktalen
und Attraktoren zusammen. Auch die Kunst geht der Spannung zwischen
Ordnung und Chaos nach.

2.2 Selbstähnlichkeit bei
fraktalen Gebilden
Schon um 1900 fand der Mathematiker Koch ein fraktales
Gebilde, indem er eine gegebene Strecke drittelte und über dem mittleren
Drittel ein gleichseitiges Dreieck errichtete. Mit den entstandenen
vier gleich langen Strecken machte er nun dasselbe wie mit der Ausgangsstrecke,
usw. Wenn man von einem gleichseitigen Dreieck ausgeht, entsteht ein
schneeflockenähnliches Gebilde (Schneeflockenkurve) das, obwohl geschlossen,
unendlich lang ist.
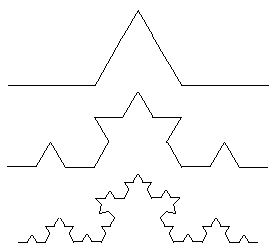

Die entstehenden Formen sind selbstähnlich. Ein Figur
heisst selbstähnlich, wenn Teile der Figur kleine Kopien der ganzen
Figur sind. Farne zeigen z.B. als Ganzes, in den Verstrebungen und
den Unter-Verstrebungen ebenfalls Selbstähnlichkeit. Ein mit einem
Fraktal-Programm auf dem Bildschirm gezeichnetes Farnblatt lässt sich
kaum von einem echten unterscheiden. Andere Beispiele aus der Natur:
Blumenkohl, die Zweige eines Baumes, …
| «Sie werden es riskieren, ihre kindlichen Vorstellungen
von Wolken, Galaxien, Blättern, Federn, Blumen, Felsen, Bergen,
Sturzbächen, Teppichen, Steinen und vielen anderen Dingen
zu verlieren. Es wird kein Zurück zu ihrer alten Auffassung
dieser Dinge mehr geben.» (Michael F. Barnsley) |

2.3 Wie lang ist die Küste Grossbritanniens?
ähnliche Erscheinungen haben wir, wenn wir die Länge einer
Küste berechnen wollen und die Feinheit bis auf die Grösse eines Sandkornes
wählen. Misst man die Länge mit Stäben in Metergrösse, könnte man
sagen, die Anzahl der Stäbe, die ich benötige, um sie einmal der Küste
entlang auszulegen, entspricht der Küstengrösse Grossbritanniens.
Doch wenn man dasselbe noch einmal mit kürzeren Stäben macht, könnte
man feineren Kurven der Küstenlinie folgen. Würde diese Länge addiert,
würde eine grössere Küstengrösse herauskommen. Je kleiner die Stäbe,
desto feiner die Verästelungen, denen sie folgen können. Die Küstenlänge
wächst ins Unendliche. Diese Gebilde, wie die genannte Küste, werden
Fraktal genannt und ihre Länge wird in der fraktalen Dimension angegeben.
Vorstellbar ist diese Zahl nicht, denn in der gewohnten Sicht der
Welt kommt sie nicht vor. Es gibt keine drei Dimensionen, sondern
fraktale Gebilde haben einen Bruch (=fractus) als Zahl ihrer Dimension.
Die Küste besteht aus weiter Ferne betrachtet aus einigen grossen
Buchten - je genauer man die Küste fokussiert, desto mehr kleinere
Buchten in den grossen Buchten tun sich auf.


2.4 Nichtlineare Fraktale (Mandelbrot-
und Julia-Mengen)
2.4.1 Mandelbrot-Mengen
Die berühmtesten Vertreter dieser Gruppe von Fraktalen
sind zweifelsohne die Mandelbrot-Menge (auch M-Menge genannt) und
die Julia-Mengen (Gaston Julia, 1893-1978). Diese Mengen haben, seitdem
sie Mandelbrot Ende der 70er Jahren vorgestellt und somit der öffentlichkeit
zugänglich gemacht hat, einiges an Aufsehen erregt. Sie sind die Geburtsstätten
der berühmtesten und schönsten Fraktal-Bilder der Welt. Bis heute
haben sie viele Künstler inspiriert, die Wissenschaftler vor immer
neue Fragen gestellt und die öffentlichkeit durch ihre faszinierende
Farbenpracht und anmutig wirkende Formenvielfalt magisch angezogen.

Die Mandelbrot-Menge ist das klassische Fraktal. Es ist
einfach ein Graph in der komplexen Zahlenebene. Die x-Achse repräsentiert
den Realteil, die y-Achse den Imginärteil einer komplexen Zahl. Es
gibt keine isolierten Punkte in der komplexen Zahlenebene: Die Mandelbrotmenge
ist zusammenhängend. Die obere und untere Hälfte der Bilder sind achsensymmetrisch
zueinander. Die Hauptmotive scheinen sich zu wiederholen (aber nie
genau gleich) bei Vergrösserungen. Die Ordnung im Chaos: Fraktale
ähneln einander immer wieder selbst. Die Menge aller komplexen Zahlen
c, für die die Folge 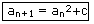 nicht gegen ƒ strebt, bilden die
sog. Mandelbrotmenge (Apfelmännchen). nicht gegen ƒ strebt, bilden die
sog. Mandelbrotmenge (Apfelmännchen).



Der Mathemaiker Mandelbrot dehnte die Untersuchungen Feigenbaums
auf die Menge der komplexen Zahlen aus und öffnete damit das Tor zur
Welt der Fraktale. Einem c entspricht nun ein Punkt der komplexen
Zahlenebene. Diesen Punkt färbte Mandelbrot genau dann schwarz, wenn
die zugehörige Iterationsfolge nicht dem Betrage gegen ƒ strebt. Die
Menge der so entstehenden schwarzen Punkte heisst Mandelbrotmenge
oder wegen ihrer Form «Apfelmännchen». Wenn man dem Rand der scheinbaren
Kurve entlang wandert, muss man sogar in den kleinsten Abschnitten
laufend seinen Kurs ändern, weshalb Mandelbrot in Anlehnung an das
Wort brechen (frangere, fractus) von einem Fraktal spricht.
| «Wolken sind keine Kugeln, Berge
keine Kegel, Küstenlinien keine Kreise. Die Rinde ist nicht
glatt - und auch der Blitz bahnt sich seinen Weg nicht gerade...
Die Existenz solcher Formen fordert uns zum Studium dessen
heraus, was Euklid als formlos beiseite lœßt, führt uns
zur Morphologie des Amorphen. Bisher sind die Mathematiker
jedoch dieser Herausforderung ausgewichen. Durch die Entwicklung
von Theorien, die keine Beziehung mehr zu sichtbaren Dingen
aufweisen, haben sie sich von der Natur entfernt. Als Antwort
darauf werden wir eine neue Geometrie der Natur entwickeln
und ihren Nutzen auf verschiedenen Gebieten nachweisen.
Diese neue Geometrie beschreibt viele der unregelmϧigen
und zersplitterten Formen um uns herum - und zwar mit einer
Familie von Figuren, die wir Fraktale nennen werden.» (Benoit
Mandelbrot 1975 - Die fraktale Geometrie der Natur) |
Seit der Entdeckung der fraktalen Geometrie vor knapp
20 Jahren ist man geteilter Meinung über ihre Bedeutung, sei es nun
in der Mathematik oder in anderen Bereichen. Die einen stempelten
Fraktale als belanglose bunte Bilder ab, die lediglich eine Laune
der Natur darstellen und keine weitere Betrachtung oder Untersuchung
wert sind. Die anderen hingegen sprühten über vor Euphorie und versprachen
sich von der neuen Welt, in die sie voller übereifer vordrangen und
die sie mit einer geradezu kindlichen Begeisterung und Faszination
erkundeten, revolutionäre neue Erkenntnisse, die die bisherige Weltanschauung
völlig verändern sollten.

2.4.2 Julia-Mengen
Nach dem französischen Mathematiker Gaston Julia sind
die Julia-Mengen benannt. Die Julia-Menge verwendet die gleiche Iterationsvorschrift
wie die Mandelbrot-Menge, nœmlich zn+1 = zn2 + c, nur bleibt hier
die komplexe Zahl c stets konstant. Dafür ist jetzt der Startwert
z0 das Interessante.


|
|
 Tweet
Tweet